こんにちは、国分寺、小平の個別指導塾、こいがくぼ翼学習塾の川東です。

都立高校入試を受けた中学３年生のみなさん、お疲れさまでした。

今日は毎年正答率の低い、都立高校入試の数学大問５（問２）の解説をしていきたいと思います！

問題についてはこちらを確認ください。

また、過去問を年度別に学習を進めたい方は、過去問をご購入ください。

東京都公立高校入試過去問題（2021年度） 価格：1100円（税込、送料無料) (2020/9/22時点) 楽天で購入

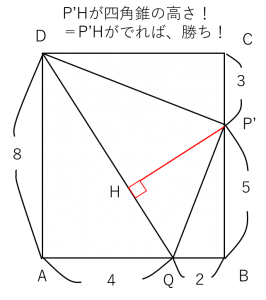
四角錐P-DQRHの体積を出す、この問題。
底面になる四角形DQRHの面積がすぐにでるのはわかると思います。

問題になるのは、この四角錐の高さ！
ここが出ずに困った受験生もいたのではないでしょうか。

そこでまず、点Pをまっすぐに上にあげ、辺BCに交わるを点P’とおきます。
点P’と垂直に交わる辺DQ上の点をHとおきます。
そうすると、辺HP’が四角錐P-DQRHの高さになります。

辺P’Hの長さを求めるため、面ABCDの図で解説していきます。

上記、辺BP’、辺P’Cのながさは、CP:PF＝３：５なので（仮定より）

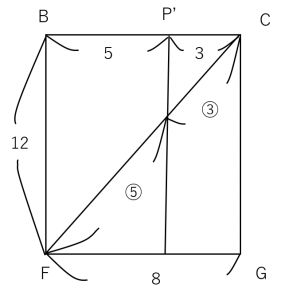
ここまでOKですか？

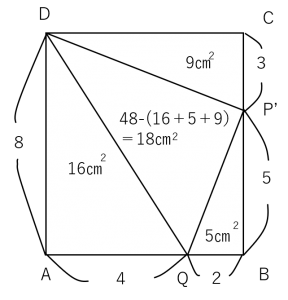
それでは、辺P’Hの長さを求めていきましょう。

作戦は、
①まず三角形DQP’の面積を求める
②底辺を辺DQにし、高さ辺P’Hの高さをもとめる

三角形DQP’の面積は以下の通りになります。

ということで、辺P’Hは、以下の通りです。

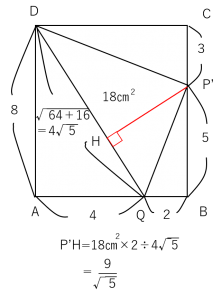
ここまできたら勝ったも同然ですね。

最後に体積をもとめましょう。

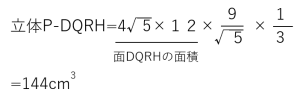
以上、いかがでしたか？

本日は、国分寺、小平の個別指導塾、こいがくぼ翼学習塾の「都立高校入試　数学　大問５（問２）の解説」についてでした！